Aperçu des sections
- Généralités
- Fiche de Contact
Fiche de Contact
Enseignante de la matière : Mr. Amor Mustapha
Maître Assistant classe "A" à l'université Ziane Achour de Djelfa.
¤ Contacts :
Par mail :
amer.mustapha@gmail.com
¤ Faculté : Sciences et technologies
¤ Département : Génie civil
¤ Public cible : Deuxième année Licence Travaux Public,
¤ Intitulé du cours : Méthode Numérique (COUR)
¤ Volume horaire global : 45 H
- Publics CIB
Publics CIB
Ce cours est dirigé aux étudiants de 2 éme Année LIC Travaux Publics (G1,G2)
- Espaces de communication généraux
- Chap1 : TD 1
Chap1 : TD 1
Chapitre 1 : Résolution de l’équation f(x)=0.
̶ Méthode de bissection.
̶ Méthode des approximations successives.
̶ Méthode de Newton.
- Chap 2 : TD 02
Chap 2 : TD 02
Résolution des systèmes d’équations linéaires.
̶ Analyse matricielle.
̶ Méthodes directes : Gauss, Jordan, Cholesky.
̶ Méthode itératives : Jacobi, Gauss, Seidel.
- Chap 03: Intégration numérique
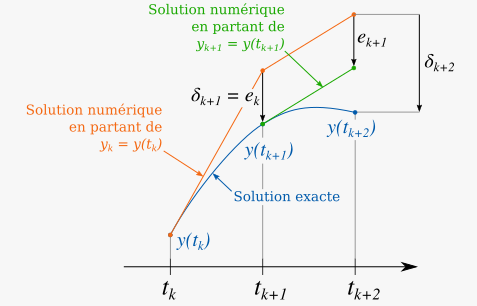
Chap 03: Intégration numérique
Intégration numérique (Newton-Cotes et Simpson).
- Chap : 04 : Méthodes d’interpolation
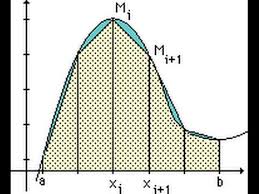
Chap : 04 : Méthodes d’interpolation
Méthodes d’interpolation.
̶ Méthode de Lagrange.
̶ Méthode de Newton.
- Réferences Bibliographie Globale
Réferences Bibliographie Globale
Références bibliographiques [1] C. Legras, Précis d'analyse numérique, Dunod, Paris 1963. [2] P. Henrici, Elements of numerical analysis, John Willey -Sons, 1967. [3] N. Bakhvalov, Méthodes numériques. Edition Mir, Moscou, 1976. [4] M. Bordeau, j. Gélinas, Analyse numérique élémentaire, Chicoutimi, 1982. [5] P. G. Ciarlet, Introduction à l’analyse numérique matricielle et à l’optimisation, Masson, Paris, 1982. - TP Méthode Numérique
TP Méthode Numérique
Les TP Méthode Numérique (TP MN) sont destiné aux étudiants de deuxième Année Licence Travaux Publics. Ils regroupent un certain nombre de méthodes étudiées dans les différents chapitres du cours de méthodes numériques.
L’objectif de ces TP est d’implémenter ou programmer sous MATLAB les différentes méthodes d'approximation et d'optimisation numérique pour résoudre les différentes probléme mathématique (l'équation linéaire et non linéaire, l'intégration, Méthodes d'interpolation...ect)
- TP 01 : Méthode de Dichotomie
TP 01 : Méthode de Dichotomie
- Programmer la méthode de résolution des équations non linéaire (méthode de Bissection).
- TP 02 : Méthode de Newton
TP 02 : Méthode de Newton
- Programmer la méthode de résolution des équations non linéaire (méthode de Newton).
- TP 03 : Méthode d'élimination de Gauss
TP 03 : Méthode d'élimination de Gauss
- Programmer la méthode de résolution des systèmes d'équations linéaires (méthode de Gauss).
- TP : 04 : Méthode de Jacobie
TP : 04 : Méthode de Jacobie
- Programmer la méthode de résolution des systèmes d'équations linéaires méthode itérative (méthode de Jacobie).
- TP N : 05 : Méthode d'intégration par Trapaz
TP N : 05 : Méthode d'intégration par Trapaz
- Programmer la méthode d'intégration numérique (méthode de Trapaz).
- TP N : 06: Méthode d'integration par Simpson
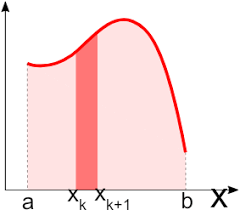
TP N : 06: Méthode d'integration par Simpson
- Programmer la méthode d'integration Numérique (méthode de Simpsin).
- TP N : 07 : Méthode d'interpolation par Lagrange
TP N : 07 : Méthode d'interpolation par Lagrange
- Programmer la méthode d'interpolation Polynomiale (méthode de Lagrange).
- Devoir N 01 Travail demandé - TD
Devoir N 01 Travail demandé - TD
Les étudiants à ce stade doivent tout d'abord pour résolus les deux excercices concernant les deux premier chapitre, et faire les devoirs qui sont détaillés en dessous.
- Devoir N 01 : TP - MN
Devoir N 01 : TP - MN
Les étudiants à ce stade doivent tout d'abord programmer les quatre TP sous Matlab (2 TP concernant la méthode de résolution d'équation non lineaire et 2TP concernant la méthode d'integration numérique),prépare les 4 TP a format papier ,vérifier s'il n y a pas d'erreur et faire les devoirs qui sont détaillés en dessous
- TP SOUS MATLAB
