2. Complexité algorithmique
Tous les algorithmes ne sont pas équivalents. On les différencie selon deux critères :
- Les temps de calcul : lents ou rapides,
- Mémoire utilisée : peu ou beaucoup.
On parle, dans ce cas, de complexité en temps (vitesse) ou en espace (mémoire utilisée).
1.1. Définitions
La complexité d’un algorithme est le nombre d’opérations élémentaires qu’il doit effectuer pour mener à bien un calcul en fonction de la taille des données d’entrée.
Pour Stockmeyer et Chandra3, "l’efficacité d’un algorithme est mesurée par l’augmentation du temps de calcul en fonction du nombre des données.". Nous avons donc deux éléments à prendre en compte :
• la taille des données ;
• le temps de calcul.
1.1.1. La taille des données
La taille des données (ou des entrées) va dépendre du codage de ces entrées. On choisit comme taille la ou les dimensions les plus significatives. Par exemple, en fonction du problème, les entrées et leur taille peuvent être :
– des éléments : le nombre d’éléments ;
– des nombres : nombre de bits nécessaires à la représentation de ceux-là ;
– des polynômes : le degré, le nombre de coefficients non nuls ;
– des matrices m × n : max(m,n), m.n, m + n ;
– des graphes : nombre de sommets, nombre d’arcs, produit des deux ;
– des listes, tableaux, fichiers : nombre de cases, d’éléments ;
– des mots : leur longueur.
1.1.2. Le temps de calcul
Le temps de calcul d’un programme dépend de plusieurs éléments :
– la quantité de données bien sûr ;
– mais aussi de leur encodage ;
– de la qualité du code engendré par le compilateur ;
– de la nature et la rapidité des instructions du langage ;
– de la qualité de la programmation ;
– et de l’efficacité de l’algorithme.
Nous ne voulons pas mesurer le temps de calcul par rapport à toutes ces variables. Mais
nous cherchons à calculer la complexité des algorithmes qui ne dépendra ni de
l’ordinateur, ni du langage utilisé, ni du programmeur, ni de l’implémentation. Pour cela,
nous allons nous mettre dans le cas où nous utilisons un ordinateur RAM (Random
Access Machine) :
– ordinateur idéalisé ;
– mémoire infinie ;
– accès à la mémoire en temps constant ;
– généralement à processeur unique (pas d’opérations simultanées).
Il est très difficile de prévoir le temps de calcul d’un programme. En revanche, on peut très bien prévoir comment ce temps de calcul augmente quand la donnée augmente.
Pour pouvoir analyser le temps de calcul, nous choisissons une opération élémentaire et nous
calculons le nombre d’opérations élémentaires exécutées par l’algorithme. Une opération élémentaire est une opération qui prend un temps constant (ou presque). Les opérations suivantes sont généralement considérées comme élémentaires :
Opérations arithmétiques (additions, multiplications, comparaisons) ;
Accès aux données en mémoire ;
Sauts conditionnels et inconditionnels ;
1.2. Mesurer le temps d’exécution
Pour calculer le temps de calcul on effectue une somme du temps d’exécution associé à chaque instruction du pseudo-code. Les opérations de base ont un temps constant, et pour les appels de sous-routines on compte le temps de l’appel (constant) avec le temps de l’exécution de la sous-routine (calculé récursivement). Le temps dépend de l’entrée (l’instance particulière du problème). On étudie généralement les temps de calcul en fonction de la « taille » de l’entrée.
Les performances d’un algorithme peuvent être jugées dans :
Le cas le plus favorable (best case), le cas le plus défavorable (worst case) ou le cas moyen (average case). On se focalise généralement sur le cas le plus défavorable (Donne une borne supérieure sur le temps d’exécution). Le meilleur cas n’est pas représentatif et le cas moyen est difficile à
calculer.
On s’intéresse à la vitesse de croissance de T(n) lorsque n croît.
Tous les algorithmes sont rapides pour des petites valeurs de n. On simplifie généralement T(n), I en ne gardant que le terme dominant.
Exemple : T(n) = 10n3 + n2 + 40n + 800
T(1000)=100001040800, 10 x 10003 = 100000000000
en ignorant le coefficient du terme dominant, asymptotiquement, ça n’affecte pas l’ordre relatif
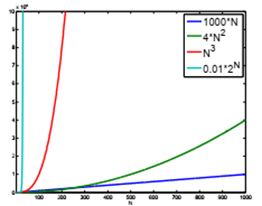
Exemple : Tri par insertion : T(n) = an2 + bn + c ! n2.
Supposons qu’on puisse traiter une opération de base en 1µs. Le temps d’exécution pour différentes valeurs de n :

La taille maximale du problème qu’on peut traiter en un temps donné sera :

Si m est la taille maximale que l’on peut traiter en un temps donné, que devient cette valeur si on reçoit une machine 256 fois plus puissante ?

1.3. Les classes de complexité
O(1) Ì O(log n) Ì O(n) Ì O(n log n) Ì O(na>1) Ì (2n)
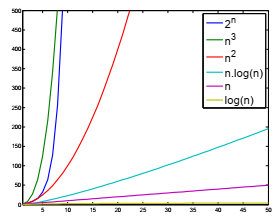
1.4. Le calcul de la complexité en pratique
Quelques règles pour les algorithmes itératifs :
- Affectation, accès à un tableau, opérations arithmétiques, appel de fonction : O(1)
- Instruction If-Then-Else : O(complexité max des deux branches)
- Séquence d’opérations : l’opération la plus couteuse domine (règle de la somme)
- Boucle simple : O(n f(n)) si le corps de la boucle est O(f (n))
- Double boucle : O(n2 f(n)) où f(n) est la complexité du corps de la boucle
- Boucles incrémentales : O(n2) (si corps O(1))
pour i <-- 1 à n
pour j <-- 1 à i
: : :
Boucles avec un incrément exponentiel : O(log n) (si corps O(1))
i <-- 1
Tantque i ≤ n
: : :
i <-- 2i
Exemple :
prefixAverages (X ) :
- Entrée : tableau X de taille n
- Sortie : tableau A de taille n tel que
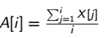
prefixAverages(X )
1 pour i = 1 à X:length
2 a <-- 0
3 pour j <-- 1 à i
4 a <-- a + X [j]
5 A[i] <-- a/i
6 renvoyer A
La complexité de cet algorithme est : O(n2)
prefixAverages2(X )
1 s <-- 0
2 pour i <-- 1 à X:length
3 s <-- s + X [i]
4 A[i] <-- s/i
5 return A
La complexité de cet algorithme est : O(n)
