2. Tri à bulles
C'est le moins performant de la catégorie des tris par échange ou sélection, mais comme c'est un algorithme simple, il est intéressant à utiliser pédagogiquement.
2.1. Spécification abstraite
Son principe est de parcourir la liste (a1, a2, ... , an) en intervertissant toute paire d'éléments consécutifs (ai-1, ai) non ordonnés. Ainsi après le premier parcours, l'élément maximum se retrouve en an. On suppose que l'ordre s'écrit de gauche à droite (à gauche le plus petit élément, à droite le plus grand élément).
On recommence l'opération avec la nouvelle sous-suite (a1, a2, ... , an-1) , et ainsi de suite jusqu'à épuisement de toutes les sous-suites (la dernière est un couple).
Le nom de tri à bulle vient donc de ce qu'à la fin de chaque itération interne, les plus grands nombres de chaque sous-suite se déplacent vers la droite successivement comme des bulles de la gauche vers la droite.
2.2. Spécification concrète
La suite (a1, a2, ... , an) est rangée dans un tableau T[...] en mémoire centrale. Le tableau contient une partie triée (en violet à droite) et une partie non triée (en blanc à gauche). On effectue plusieurs fois le parcours du tableau à trier; le principe de base étant de ré-ordonner les couples (ai-1, ai) non classés (en inversion de rang soit ai-1 > ai) dans la partie non triée du tableau, puis à déplacer la frontière (le maximum de la sous-suite (a1, a2, ... , an-1)) d'une position :
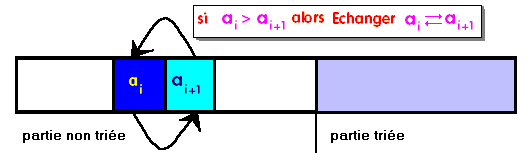
Tant que la partie non triée n'est pas vide, on permute les couples non ordonnés ( (ai-1, ai) tels que ai-1 > ai) ) pour obtenir le maximum de celle-ci à l’élément frontière. C'est à dire qu'au premier passage c'est l'extremum global qui est bien classé, au second passage le second extremum etc...
2.3. Algorithme
|
Algorithme Tri_a_Bulles |
Exemple : soit la liste ( 5 , 4 , 2 , 3 , 7 , 1 ), appliquons le tri à bulles sur cette liste d'entiers. Visualisons les différents états de la liste pour chaque itération externe contôlée par l'indice i :
i = 6 / pour j de 2 jusquà 6 faire

i = 5 / pour j de 2 jusquà 5 faire

i = 4 / pour j de 2 jusquà 4 faire

i = 3 / pour j de 2 jusquà 3 faire

i = 2 / pour j de 2 jusquà 2 faire
![]()
i = 1 / pour j de 2 jusquà 1 faire (boucle vide)
![]()
2.4. Complexité
Choisissons comme opération élémentaire la comparaison de deux cellules du tableau. |
Le nombre de comparaisons "si Tab[ j-1 ] > Tab[ j ] alors" est une valeur qui ne dépend que de la longueur n de la liste (n est le nombre d'éléments du tableau), ce nombre est égal au nombre de fois que les itérations s'exécutent, le comptage montre que la boucle "pour i de n jusquà 1 faire" s'exécute n fois (donc une somme de n termes) et qu'à chaque fois la boucle "pour j de 2 jusquà i faire" exécute (i-2)+1 fois la comparaison "si Tab[ j-1 ] > Tab[ j ] alors".
La complexité en nombre de comparaisons est égale à la somme des n termes suivants (i = n, i = n-1,....)
C = (n-2)+1 + ([n-1]-2)+1 +.....+1+0 = (n-1)+(n-2)+...+1 = n(n-1)/2 (c'est la somme des n-1 premiers entiers).
La complexité en nombre de comparaison est de de l'ordre de n², que l'on écrit O(n²).
Choisissons maintenant comme opération élémentaire l'échange de deux cellules du tableau. |
Calculons par dénombrement le nombre d'échanges dans le pire des cas (complexité au pire = majorant du nombre d'échanges). Le cas le plus mauvais est celui où le tableau est déjà classé mais dans l'ordre inverse et donc chaque cellule doit être échangée, dans cette éventualité il y a donc autant d'échanges que de tests.
La complexité au pire en nombre d'échanges est de l'ordre de n², que l'on écrit O(n²).
